Clustering

Clustering is a fundamental task in data analysis and data mining. It involves grouping objects or observations into non-overlapping clusters.

In the field of data mining, clustering is used for customer and market segmentation, medical diagnostics, social and demographic studies, assessing creditworthiness of borrowers, and many other areas.

To illustrate the task, the "Fisher's Iris" dataset is commonly used. This dataset was used by R. Fisher to demonstrate the functionality of his developed discriminant analysis method.

Launch demo

Download example

Algorithm Description

1. Data Import

Import of «Fisher's Iris» dataset

The set consists of data on 150 iris specimens. Four characteristics were measured for each (in centimeters).

Name	Label
sepal_length	Sepal Length
sepal_width	Sepal Width
petal_length	Petal Length
petal_width	Petal Width

2.1 EM Clustering

The basis of EM clustering is the assumption that any observation belongs to all clusters, but with varying probabilities. An object should be assigned to the cluster for which this probability is higher.

a) EM Clustering Settings

The following settings are established for the EM Clustering node:

For fields sepal_length, sepal_width, petal_length, petal_width - assignment is Used
In the parameter Given number of clusters, the value is set to 3
Other settings are default

If the settings are changed, retrain the model.

Interpretation of Results

b) Output Set Cluster Division

In the output set, two new columns appear, which are added to the original set:

Cluster Number
Membership Probability

Cluster Number	Membership Probability	Sepal Length	Sepal Width	Petal Length	Petal Width	Class
1	1.00	5.10	3.50	1.40	0.20	Iris-setosa
...	...	...	...	...	...	...
2	1.00	7.0	3.20	4.70	1.40	Iris-versicolor
...	...	...	...	...	...	...
0	1.00	5.90	3.0	5.10	1.80	Iris-virginica

c) Visualization of Results

The results of EM Clustering can be viewed in the Cluster Profiles visualizer:

Picture 1. Cluster Profiles

In the Cluster Profiles visualizer, it is possible to view statistical indicators that can be used to compare clusters with each other:

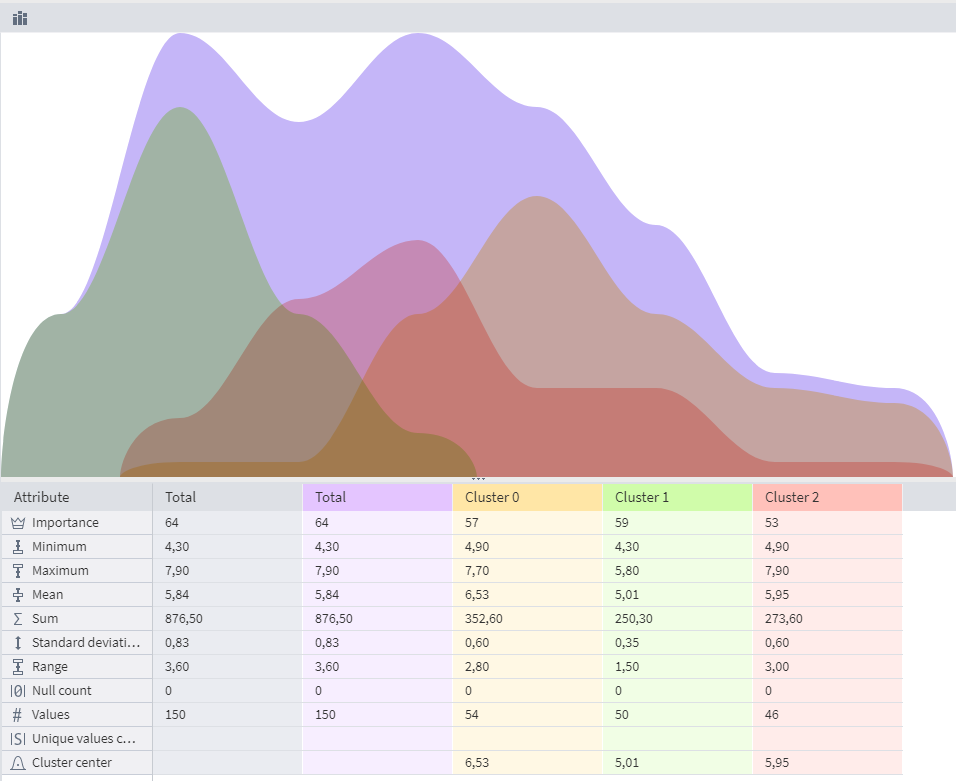
Picture 2. Cluster Profiles (comparison)

The algorithm identified 3 clusters, which coincide with the number of original classes and are approximately equal, which indicates the good performance of the EM clustering algorithm.

2.2 K-means Clustering

K-means clustering is used in the case when the number of clusters is known.

a) K-means Clustering Settings

The following settings are established for the K-means Clustering node:

For fields sepal_length, sepal_width, petal_length, petal_width - assignment is Used
In the parameter Given number of clusters, the value is set to 3
Other settings are default

If the settings are changed, retrain the model.

Interpretation of Results

b) Output Set Cluster Division

In the output set, two new columns appear, which are added to the original set:

Cluster Number
Distance to Cluster Center

Cluster Number	Distance to Cluster Center	Sepal Length	Sepal Width	Petal Length	Petal Width	Class
2	0.23	5.10	3.50	1.40	0.20	Iris-setosa
...	...	...	...	...	...	...
0	0.95	7.0	3.20	4.70	1.40	Iris-versicolor
...	...	...	...	...	...	...
0	1.06	5.90	3.0	5.10	1.80	Iris-virginica

c) Visualization of Results

The results of K-means Clustering can be viewed in the Cluster Profiles visualizer:

Picture 3. Cluster Profiles

In the Cluster Profiles visualizer, it's possible to view statistical indicators by which clusters can be compared with each other:

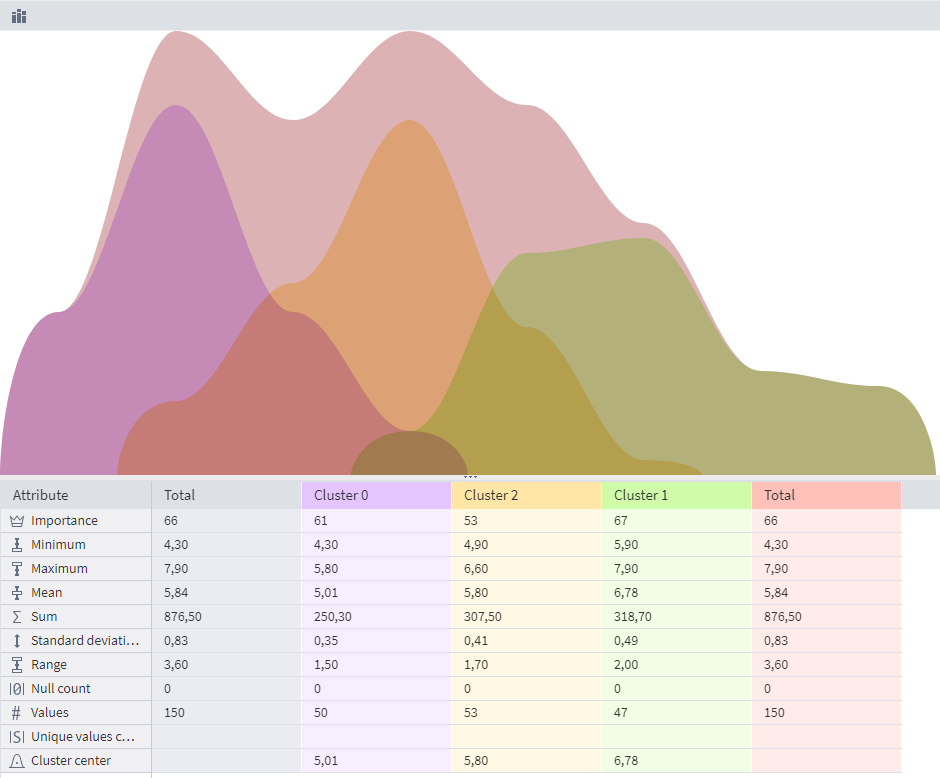
Picture 4. Cluster Profiles (comparison)

The algorithm identified 3 clusters, which correspond to the number of classes in the input dataset. However, each cluster contains a significantly different number of objects. Thus, k-means clustering is less accurate than EM.

2.3 G-means Clustering

G-means clustering is used when the initial number of clusters is unknown. The algorithm automatically determines the appropriate number of clusters.

a) G-means Clustering Settings

The following settings are established for the G-means Clustering node:

For fields sepal_length, sepal_width, petal_length, petal_width - assignment is Used
The flag "Automatic determination of the number of clusters" is set.
Other settings are default

If the settings are changed, retrain the model.

Interpretation of Results

b) Output Set Cluster Division_**

Two new columns have been added to the original dataset in the output:

Cluster number
Distance to the cluster center

Cluster Number	Distance to Cluster Center	Sepal Length	Sepal Width	Petal Length	Petal Width	Class
0	0.23	5.10	3.50	1.40	0.20	Iris-setosa
...	...	...	...	...	...	...
1	1.23	7.0	3.20	4.70	1.40	Iris-versicolor
...	...	...	...	...	...	...
1	0.56	5.9	3.0	5.10	1.80	Iris-virginica

c) Visualization of Results

The results of G-means Clustering can be viewed in the Cluster Profiles visualizer:

Picture 5. Cluster Profiles

In the Cluster Profiles visualizer, it's possible to view statistical indicators by which clusters can be compared with each other:

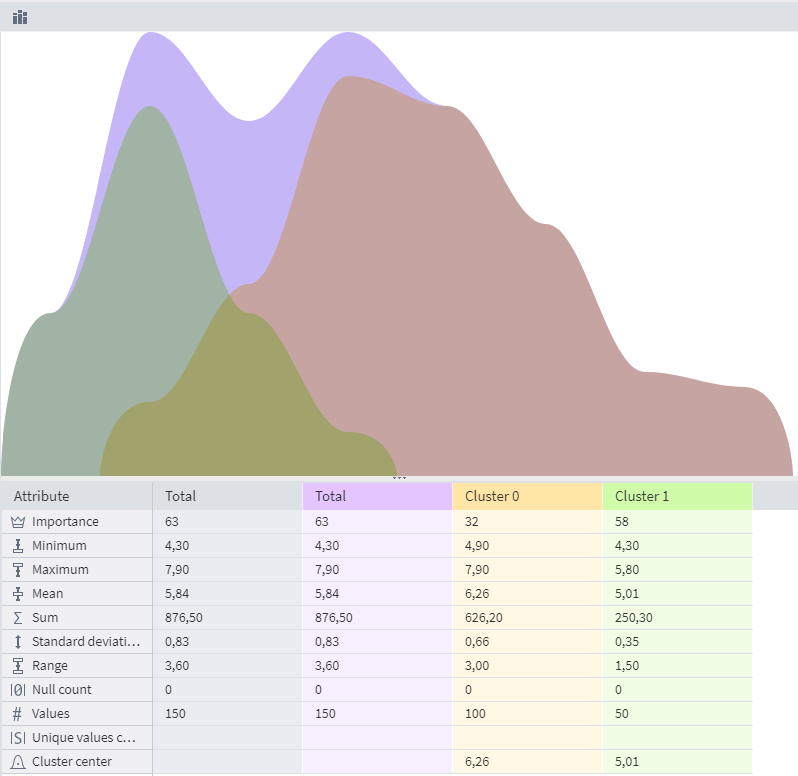
Picture 6. Cluster Profiles (comparison)

The algorithm identified 2 clusters, which, firstly, do not match the number of classes in the original dataset, and secondly, resulted in an uneven distribution. Thus, g-means clustering has been found to be the least accurate, and its results can be considered unsatisfactory.

data mining

Clustering

Algorithm Description

1. Data Import

2.1 EM Clustering

Interpretation of Results

2.2 K-means Clustering

Interpretation of Results

2.3 G-means Clustering

Interpretation of Results

results matching ""

No results matching ""